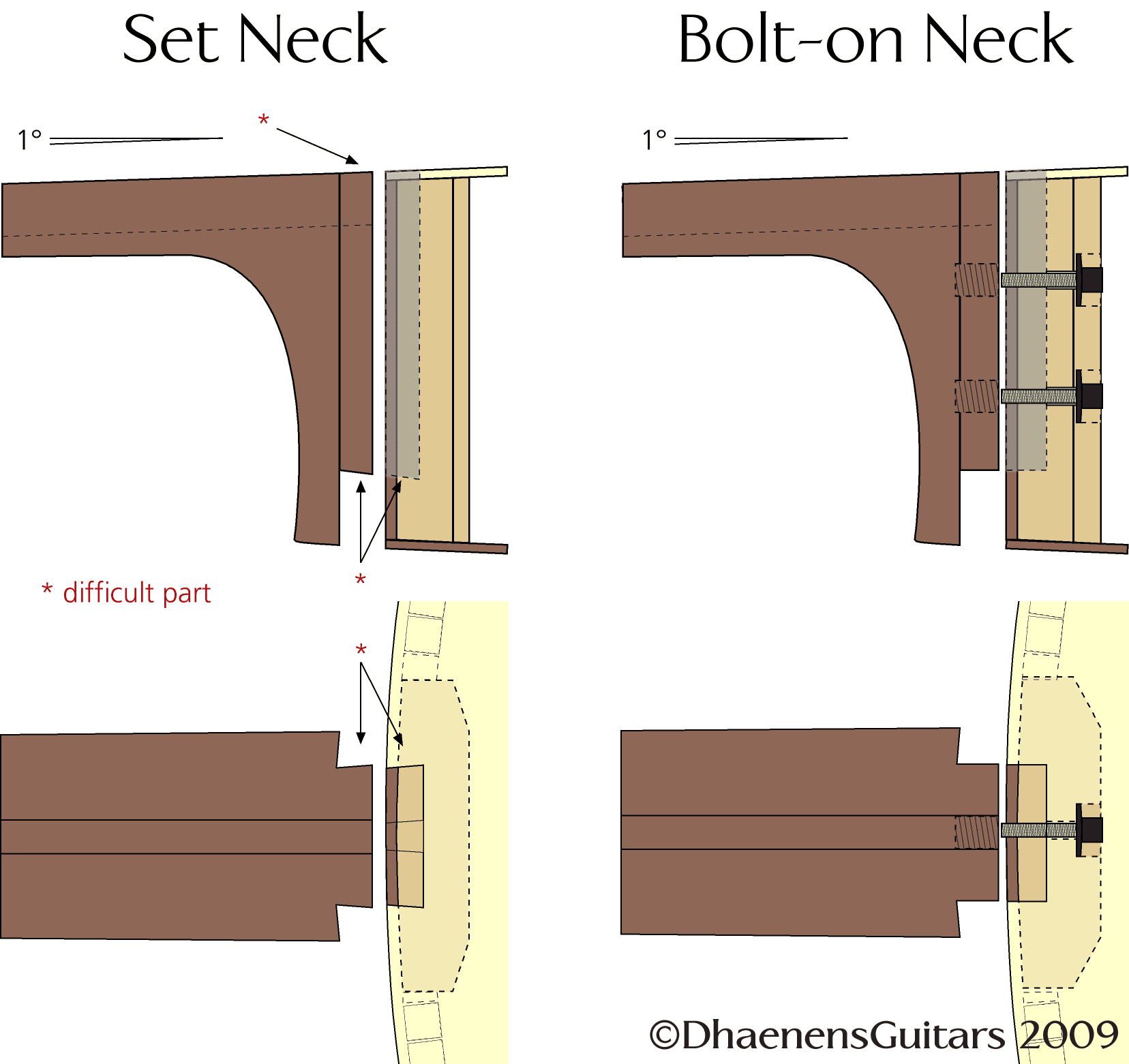
ARTIKELS
Guitars are designed for the 12-tone equal tempered tuning (12-TET). In a 12-tone equal tempered tuning, an octave is divided in 12 semitones at an equidistance of each other: C, C# or Db, D, D# or Eb, E, F, F# or Gb, G, G# or Ab, A, A# or Bb, B.
12-tone equal tempered tuning assumes that e.g. C# is soundwise exactly in the middle of C and D. As you could have guessed, in real life it’s not, it’s only in the mathematical middle and soudwise a bit on the sharp side.
Guitars and all other instruments are tuned at A4= 440 Hz. In 1939 musicians world-wide came to a consensus on that pitch. Before that time, the pitch had been 435 Hz, 374 Hz (1648) and 503 Hz (1361) but those were merely guidelines. Each maestro was free to compose or direct at a lower or higher pitch.
(Hz is the unit to express the number of oscillations of pressure in a sound wave. 440Hz means that there are 440 oscillations per second.)
When you pull an unfretted A-string on a tuned guitar, you’ll hear 110 Hz. When you fret that string at the 12th fret, you’ll hear 220 Hz. That’s exactly the double. Double or half the Hz of any tone is called an octave. Fret that string at the 24th fret and you’ll hear 440 Hz, again one octave higher or 2 octaves higher than the tone of the unfretted string. What you have done each time, is shorten the string by half. A shorter string vibrates at a higher speed thus producing more oscillations per second. A string at 440 Hz oscillates twice as fast as a string of double that length.
The guitar is fretted so we can easily pick the correct notes. Those frets are laid out according to a simple calculation.
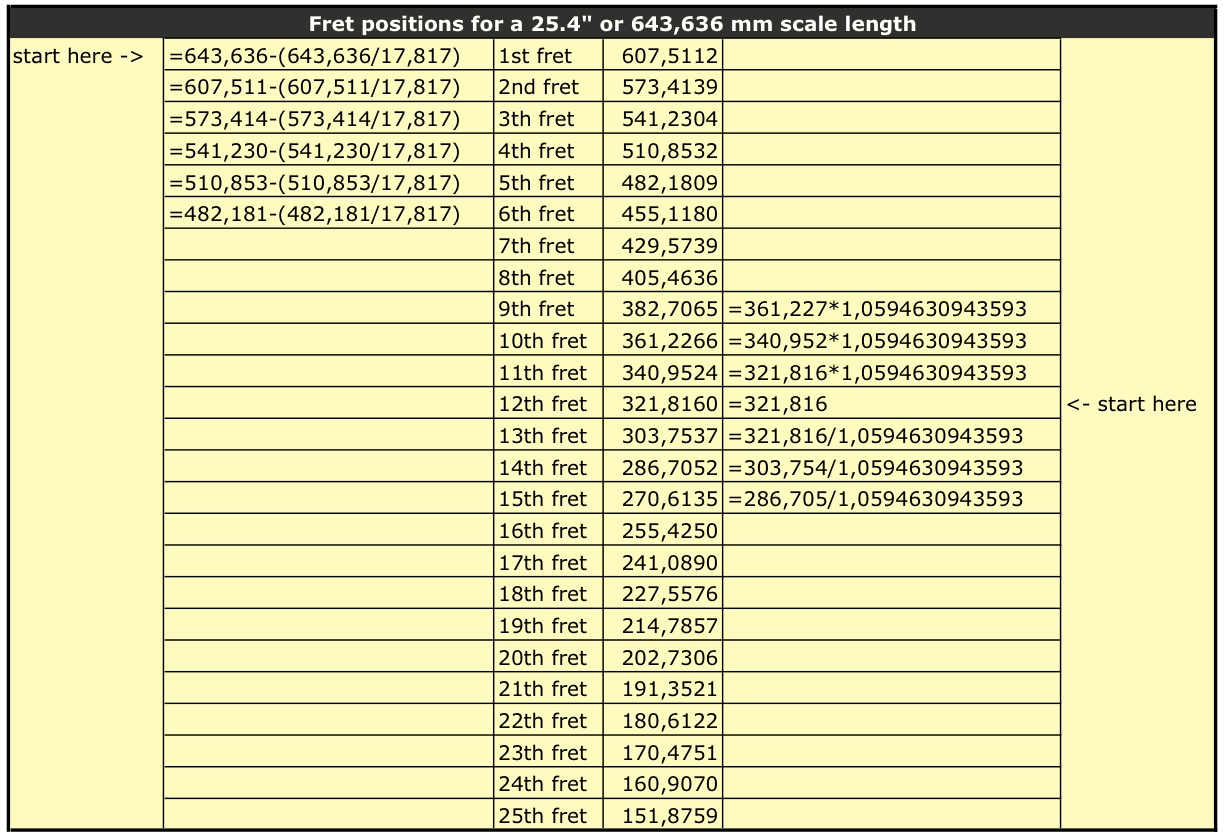
Assume that the scale length of your guitar is 25.4″ (actually it’s 25,34″) or 643,636 mm. The scale length is the distance between the nut and the top of the saddle. The 12th fret will be exactly at 12.7″ (25.4″/2) or 321,818 mm. And since an octave in a 12-TET scale is divided in 12 semitones at equidistance of each other, the math should be fairly simple, no? Alas, dividing 12.7″ by 12 won’t do. That is because we can’t use the distance as input for our calculations, we have to use the frequences. In a 12-TET scale, the ratio of frequencies between two adjacent semitones is the twelfth root of two. And the twelfth root of two is 1.0594630943593.
So starting from the 12th fret, the exact position of the other frets is easily calculated by multiplying or dividing the position of a (previous) fret with 1.0594630943593.
The position of the 11th fret is 340,9543 mm (321,818 * 1,0594630943593); the position of the 10th fret is 361,2626 mm (340,954294100521 * 1,0594630943593); that of the 13th fret is 303,7557 mm (321,818 / 1,0594630943593) and so on.
Another way to determine the fret positions is by using the constant 17.817. The scale length divided by this value gives us the distance from the nut to the first fret.
The following table will make it more clear: